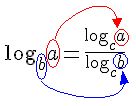Logaritmo

Considerando a e b  dois números reais  e positivos, sempre com a diferente de 0 , define-se logaritmo de b(logaritmando) na base a, qual número deve-se incluir no expoente de a afim de termos b como resultado.

Assim: a^x = b , então temos que 

Com as condições de .

I) , sendo que 3 é o logaritmo, 2 é a base e 8 é o logaritmando.
pois temos que 2³ = 8.

II) , sendo que –3 é o logaritmo, 3 é a base e 1/27 é o logaritmando.
pois temos que 3^-3 = 1/27 .

→ Antilogarítimo é definido como sendo: 
Exemplo:

I) 

Propriedades zero ( que são conseqüência direta da definição)

1º Propriedade (propriedade do produto).

2º Propriedade (propriedade do quociente).

3º Propriedade (propriedade da potência).

Conseqüência da 3º propriedade :

4º Propriedade (propriedade da mudança de base).

→ Colog, definição:

Mudança de Base

Em muitos casos na resolução de operações envolvendo logaritmos, é viável e se faz necessário a utilização de técnicas capazes de nos fornecer de forma precisa e direta o conjunto solução de uma questão, uma dessas “técnicas” é conhecido como mudança de base de um logaritmo, na qual veremos a seguir.

Vejamos:

Observe que inicialmente temos um logaritmo qualquer representado por uma base “b” e o logaritmando “a” , fazendo a mudança de base , vamos transformar esse logaritmo em um quociente de um logaritmo formado por um base “c” .Podemos perceber que tanto “a” quanto “b” passam a ser o logaritmando formado pela base “c”.

Para facilitar o entendimento da mudança de base, iremos aqui resolver alguns exercícios. Lembrando sempre que para que um logaritmo exista, sua base tem que ser maior que 0 e diferente de 1 (b>0 e b=/=1) e também é importante lembrar que seu logaritmando tem que ser maior que 0(a>0).

1) Calcule pela mudança de base o valor de  Log₄64 .

Podemos escrever que;

Log₄64 = log₂ 64 / log₂ 4

Calculando separadamente, temos;

Log₂64 = 2^x = 2⁶; x=6

Log ₂4 = 2^x = 2²;  x=2

Portanto, x =6/2 = 3

Para provarmos essa técnica poderíamos conferir a resposta pela definição do logaritmo, sendo 64 um múltiplo de 4, sua forma fatorada é   64= 4³

Portanto  Log₄64 = x  ;  4^x=4³, x=3

2) Sabendo-se que log₁₀ 2 =0,301  e log₁₀ 3=0,477 , pede-se. Calcule o valor de  Log₉512

Podemos escrever que;

Log₉512= log₁₀512/log₁₀9

Calculando separadamente, temos;

Log ₁₀512= Log ₁₀2⁹= 9 x log₁₀2 =9x0, 301=2,709

Log₁₀9= Log₁₀3²= 2xlog₁₀3=2x0, 477=0, 954

Reescrevendo (Efetuando o quociente);

Log₉512= 2,709/0,954 =2,839(Resultado aproximado).